PROBLEM 2
 | |
ŞOK FAKTÖRÜ (IMPACT FACTOR) PROBLEM 1 de yüksekten düşen bir cismin kirişte yaptığı deformasyonu daha kolay hesaplamak için düşen cismin kirişe çarptıktan sonra kiriş ile birlikte almış olduğu seğim miktarı kadar yolu enerji denkleminde göz ardı etmiştik. Eğer düşme mesafesi çok uzun ve yay katsayısı büyükse seğim kadar ilave yolun sonuca etkisi ihmal edilebilecek kadar küçük olur. Ancak düşme mesafesi kısa ve yay katsayısı küçükse seğim kadar ilave yolun dikkate alınması önem kazanır. Seğim kadar yolun düşme yüksekliği ile birlikte enerji denkleminde yer alması için enerji denkleminin aşağıdaki gibi yazılması gerekir. m*g*(h+x)= 1/2 k x2 |
m kütlesi kirişin ortasına elle koyulduğunda uygulanabilecek yay formülünden m*g=k*y Yukarıdaki iki denklemin birlikte çözümünden aşağıdaki denklem elde edilir. x2-2yx-2yh=0 İkinci derceden bu denklemin x için çözümünden. x=y*(1+(1+2h/y)1/2) x/y=1+(1+2h/y)1/2 | 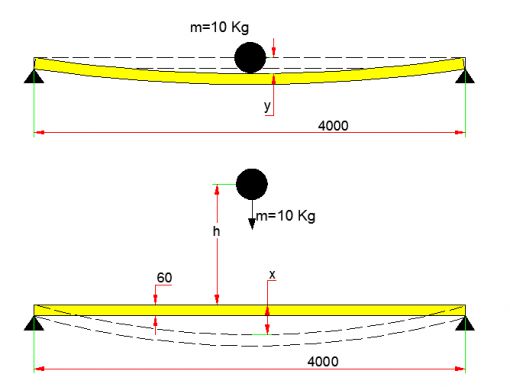 | |
elde edilir. Bu deklemde x/y= n olarak tanımlanır ve sağda verilen şok faktörü elde edilmiş olur. | 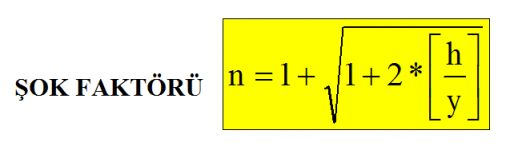 | n: Şok faktörü |
Şok faktörü son derece sade bir formül olup bu faktörün elde edilmesi için sadece iki parametreye ihtiyaç vardır. Birincisi cismin düşme yüksekliği h. İkincisi ise cismin kiriş üzerinde düşme noktasına elle koyulması ile elde edilecek seğim miktarı olan y değeridir. Bkz üstteki resim | ||
Şok faktörünü kullanarak hem çarpmadan sonra kirişte gerçekleşecek toplam seğim miktarı x hemde bu etkiyi oluşturabilecek kuvvet F elde elde edilir. | X=n*y F=n*W | |
ÖRNEK PROBLEM Soru : 4 metre boyunda ve 40X60mm2 kesit alanı olan, başlar mafsal destekli bir kirişin tam ortasına kütlesi 10 kg olan bir cismin 0.5 metre yüksekten düşmesi ile oluşan seğim miktarı ne kadar olur. Cevap: Önce kütlesi 10 Kg olan cismin kirişin tam ortasına yavaşça koyulması ile oluşan seğim miktarını bulalım. Başlar mafsal destekli kirişte yükün ortadan basması ile ortaya çıkan | ||
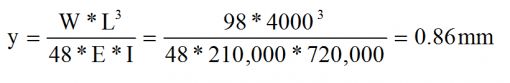 | Soldaki formülde W=m*g=10*9.8=98 N | |
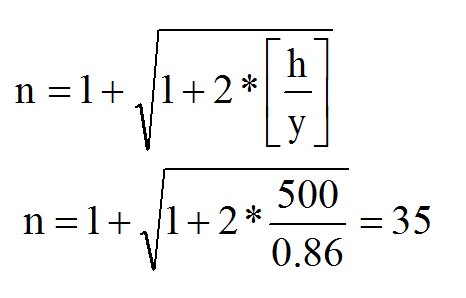 ==> n=35 (Şok faktörü) | ||
Çarpma sonucunda ortaya çıkan seğim x=n*y = 35*0.86 = 30 mm 30 mm seğimi oluşturabilecek kuvvet F=n*W= 35*98= 3430N Bu kuvvetin oluşturabileceği max. moment Mmax= F*L/4 = 3430*4000/4= 3,430,000 N-mm Nominal eksen kirişin tam ortasından geçtiğinden c=60/2= 30 mm | Çarpma sonrası kirişte oluşan gerilim (Bkz. Önemli formüller)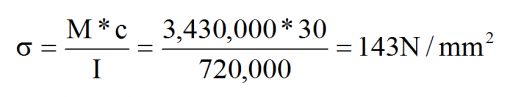 | |
Kiriş malzemesinin St37-2 olduğunu kabul edersek, bu malzemenin çekme dayanımını TABLO dan Sy=215 N/mm2 olarak tespit ederiz. Bu değer (215 N/mm2) > 143 N/mm2 olduğundan bu deformasyon elastik bölgede olur ve kiriş esnedikten sonra eski haline döner. | 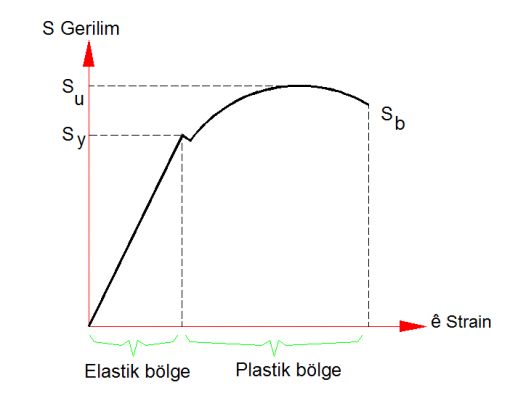 | |
| 0000000000000000000000000000000000000000 | ||
| GERİ DÖN | ||

