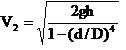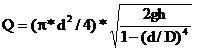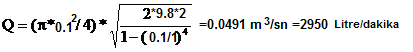PROBLEM 6
PROBLEM 6 Problem 4 de verilen dik tankın içindeki su seviyesinin (h) değişmeden kalması için tanka doldurulacak sıvı debisi ne kadar olmalıdır. Bu problem basit ama sık karşılaşılan bir problem olduğu için vermekte yarar gördüm. Tank seviyesinin sabit kalması için giriş ve çıkış su debileri eşit olmalıdır. Aksi halde tank taşar veya seviyesi düşer. | |
Yani ; ( π D2 / 4) *V1 = ( π d2 / 4) *V2 Bu formülden V1=(d/D)2*V2 (Formül 1) Not: Tankın üst yüzeyinde belli bir kinetik enerji olması nedeni ile seviye değişmese bile V1 hızı sıfırdan büyüktür Bu tip problemlerde her zaman kullanılan denklem meşhur Bernoulli denklemidir.(Bkz.Önemli formüller) P1 +(1/2) ρV12 + ρ g Z1 = P2 +(1/2) ρV22+ ρgZ2 Problemimizde tank atmosfere açık olduğu ve atmosfere açık bir yere boşaltma yaptığı için P1=P2 dir Denklemi sadeleştirirsek (1/2) ρV12 + ρ g( Z1 – Z2) = (1/2) ρV22 Seviye farkı h olduğu için denklem aşağıdaki formu alır (1/2) ρV12 + ρ g h = (1/2) ρV22 (Formül 2) Yukarıda bulunan Formül 1 ve Formül 2 yi birlikte tanktan boşalma hızı V2 için çözersek | 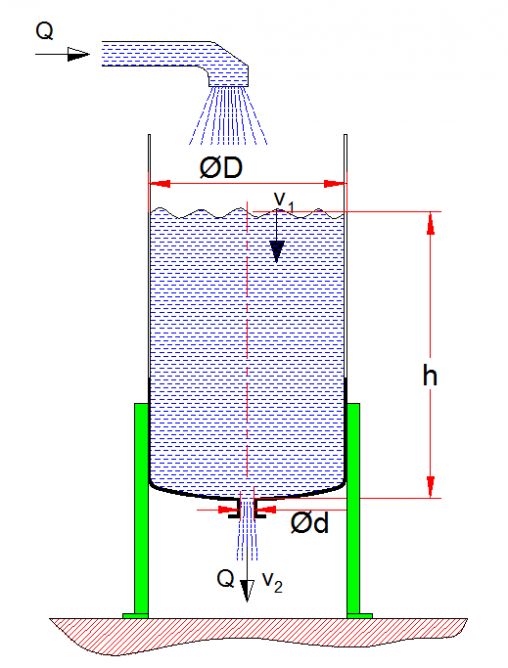
|
Q= A2* V2
| |
Örnek Çapı 1
metre olan tank içideki su seviyesinin 2 metre de sabit tutulması
isteniyor. | |
D= 1
metre |
|
Yukarıda verilen problemde tank çapı D çıkış çapı d ölçüsünden 10 misli fazla ise tank yüzeyi hızı V1 sıfır kabul edilebilir. V1 sıfır kabul edildiği zaman bernouli denkleminden Bu durumda örnek problemde ki Q için sonuç hemen hemen aynı olur.
| |