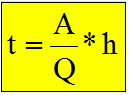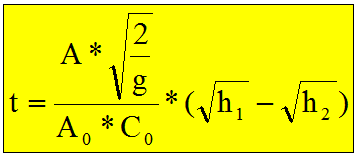PROBLEM 4
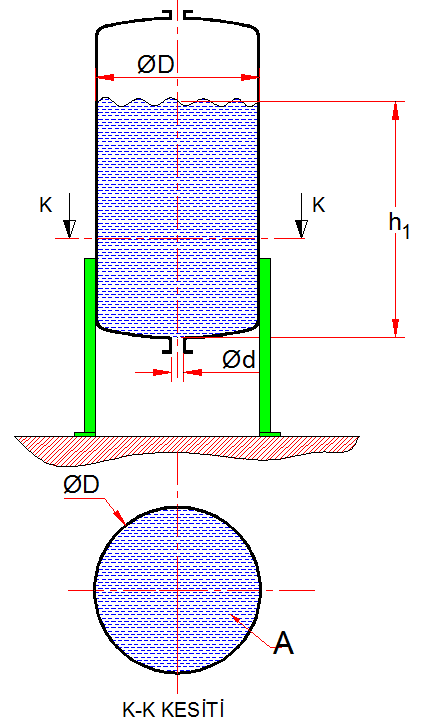
D çapında silindirik bir tank h1 seviyesine kadar akıcı (Newtonian) bir sıvı ile doludur. İlk bakışta basit bir soru gibi gözüküyor. Ama hiçte öyle
değil. Yani Q=V/t → t= V/Q Yukarıda bulunan denklemi zamanın ve sıvı yüksekliğinin |
Q= Boşalma debisi (m3/sn) A0= çıkış deliğinin kesit alanı (m2) C0= Orifis katsayısı (Bu tip orifislerde g= yerçekimi ivmesi (9.8 m/sn2) h1= Sıvının ilk seviyesi (m) h2= Sıvının son seviyesi (m) | |
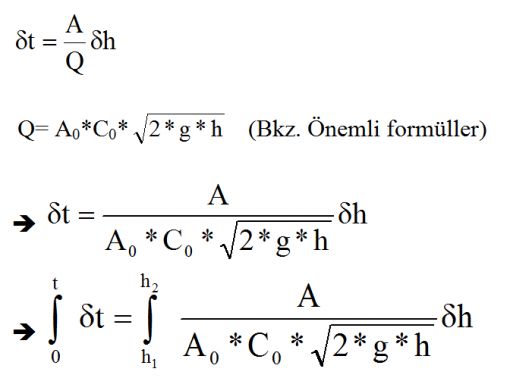
Yukarıdaki denklemin integral çözümünden |
| |
Not: Bu formülde sadece A kesiti olduğu için
| ||
| (İntegral çözümleri için http://integrals.wolfram.com sitesini kullanabilirsiniz) | ||
Çapı 6
metre ve boyu 10 metre olan bir tankın içinde bulunan sıvının seviyesi
altındaki boşaltma deliğinden 7
metre yukarıdadır. | ||
Tankın kesit alanı D=6 m => A= 28.27 m2 Boşalma deliğinin alanı d=0.15 m => A0= 0.0177 m2 Tank içindeki sıvının ilk seviyesi h1=7.3 m Tank içindeki sıvının son seviyesi h2=0 m (Tamamen boşalacak) Boşalma deliği orifis katsayısı C0=0.6 Yukarıda verilen t formülünden | ||
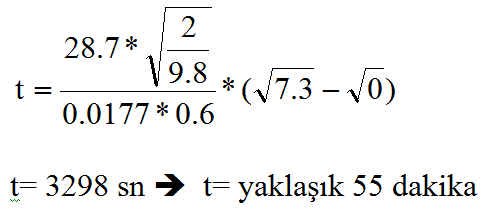 | ||
Aynı büyüklükte yatık konumdaki tankın boşaltılması ne kadar zaman alır. BAKINIZ PROBLEM 5
| ||
| ||